Summer 2025 Mathematics Research Information
The Department of Mathematics encourages student research in a number of ways. Mathematics majors are required to complete a capstone project by either joining a year-long team Clinic project or working with a faculty advisor on a thesis project. The department also offers summer research opportunities hosted at HMC.
2025 Summer Research
Hosted at HMC
Hosted Elsewhere
- UCLA REU in Applied and Computational Mathematics (Cofounded by Professor Bernoff!)
- Other Math REU’s
Faculty Research Interests
Arthur Benjamin
Combinatorial proofs of Fibonacci identities and other interesting sequences; Mathematics of games, gambling, and puzzles.
Andrew Bernoff
Modeling of Physical and Biological Systems, Applications of Dynamical Systems, Fluid Mechanics, Self-Similarity and Scaling
Topic I: Models of Discrete and Continuous Swarming
Overview:Swarming of organisms is a ubiquitous phenomena in the world around us; flocks of birds, schools of fish and locust swarms are examples of systems we have considered. There are several projects available that fit in as part of an ongoing effort to understand the dynamics of increasingly detailed models of these social structures. Some sample projects are listed below.
Background Needed:Some PDE’s, comfort with numerical methods and computing.
Skills Learned:Modeling of biological systems, familiarity with energy and variational methods, bifurcation theory, integral equations, numerical and asymptotic methods.
Sample Project: Mathematical Modeling of Heterogeneous Swarms
Most swarm models assume that all individuals are identical and interchangeable but in nature individuals are heterogeneous. For example, if one assumes that visual attraction to larger individuals is stronger in a popular model of fish schools, larger individuals drift to the swarms periphery and smaller individuals drift to the interior. This behavior is observed in nature and biologically can be interpreted as protection of juveniles. This project will be a combination of biological modeling, numerical simulation, and mathematical analysis of models of heterogeneous swarms.
Sample Project: Bifurcation Problems in Discrete and Continuous Swarms
Discrete, Agent-based models of swarms often exhibit steady states that while irregular suggest highly symmetric states such as spheres and rotating mills. One can study these problems by deriving continuous (PDE) versions of the agent-based models and looking for a hierarchy of bifurcations and steady-states. This project will touch on both kinetic theory of particle systems and dynamical systems methods for examining bifurcations with symmetry.
Sample Project: Mathematical Modeling of Nearest Neighbor Interactions in Two Dimensions
The most popular continuum models of biological aggregation have an undesirable feature that the maximum density observed in equilibrium configurations is proportional to the biomass. Recently, we have examined a strategy in one dimension for modeling nearest neighbor interactions that leads to aggregations with a maximum density. In higher dimensions, this strategy is more difficult to implement because individuals are not well-ordered and the idea of nearest neighbors is ill-defined. In this project we will use a Voronoi decomposition to identify nearest neighbors and to derive appropriate continuum models in two dimensions.

Topic II: Kinetic Monte Carlo Methods for Diffusive Capture
Description:Consider the pistil of a flower waiting to catch a grain of pollen, a lymphocyte waiting to be stimulated by an antigen to produce antibodies, or an anteater randomly foraging for an ant nest to plunder. Each of these problems can be modeled as a diffusive process with a mix of reflecting and absorbing boundary conditions. One can characterize the agent (pollen, antigen, anteater) finding its target (pistil, lymphocyte, ant nest) as a first passage time (FPT) problem for the distribution of the time when a particle executing a random walk is absorbed. Numerically simulating these problems involves analytically solving the diffusion equation in a variety of domains and then sampling the exit time distributions associated with the solutions. Our simulations and asymptotics for these problems are slowly and steadily reproducing more realistic geometries for the biological capture problems they model.
Topic III: Energy Driven Pattern Formation
Description:Many physical systems are driven by pairwise particle interactions; for example in thin liquid and solid layers, pairs of molecules interact electromagnetically. In swarming, the gathering of insects is often modeled via a pairwise social force. These systems can exhibit elaborate changes of morphologies as system parameters change. An example of this is the circle-dogbone-labyrinth transition seen in Langmuir films as the domain size increases (see Figure). In this project we will investigate the relationship between theses morphology changes and the form of the pairwise potential via energy methods and bifurcation theory. While many examples of these transitions have been observed for specific systems, characterizing these transitions for generic potentials remains a fertile area for study.
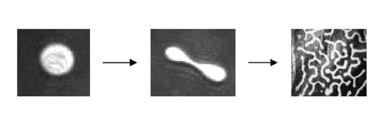
Background Needed:Some PDE’s, comfort with numerical methods and computing.
Skills Learned:Familiarity with energy and variational methods, bifurcation theory, integral equations, numerical and asymptotic methods.
If you are interested send me an e-mail (ajb@hmc.edu).
Alfonso Castro
Solvability of ordinary and partial differential equations using both elementary integration methods and functional analytic tools. The intermediate value theorem and its generalizations to several variables, the contraction mapping principle, variational methods, and the implicit function theorem are examples of techniques used in these studies. Go to Mathscinet to see the nature of my research. Papers with C.M. Tan, B. Preskill and E. Fischer are the result of senior thesis work at HMC.
Lisette de Pillis
Mathematical biology, including tumor modeling, immunology modeling, blood coagulation modeling, diabetes treatments, optimal control, HIV/AIDS modeling, epidemiology modeling; numerical linear algebra.
Preparation needed: Linear algebra; Differential equations; some coding (Matlab, e.g.).
Possible Capstone Projects
- Diabetes type 1: modeling effective treatment and prevention strategies with differential equations. Strong computing skills as we as exposure to Matlab and to mathematical modeling required.
- Cancer/immunology/cancer-treatment modeling with differential equations.
- Cancer/immunology/cancer-treatment modeling with cellular automata.
- Modeling blood clotting mechanisms and treatments with differential equations.
- Epidemiological modeling with differential equations.
- Exploration of large data sets (gene expression, flow cytometry data) to identify/predict disease stage progression.
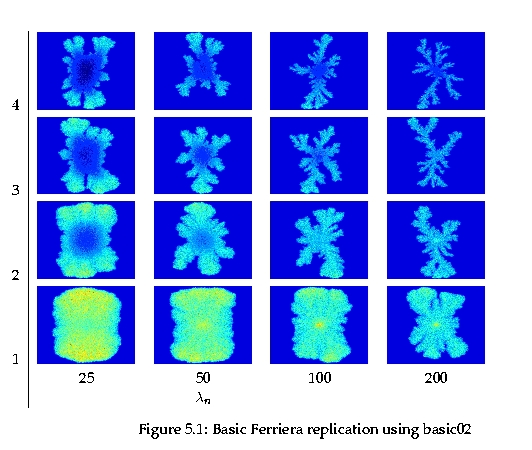
Figure: In this simulation, we explore the effects of “tumor gluttony” (how rapidly tumor cells consume nutrients relative to healthy cells) on tumor morphology. We see that increased tumor gluttony leads to tumors that are less compact and more papillary. Papillary tumors tend to be more dangerous.
If you wish to discuss any of these projects, feel free to contact me at depillis@g.hmc.edu. Please put RESEARCHINTEREST in your subject line to make sure I see your email.
Weiqing Gu
- Differential geometry, Grassmann manifolds, characteristic classes and applications to string theory.
- Big data analysis. There are big data problems everywhere in this world. There is an urgent need to apply machine learning and advanced mathematical techniques to extract patterns and insights from large and complex collections of digital data and to achieve data-to-decision since traditional statistical methods do not suffice. In this faculty-student research or a student senior thesis project we will identify patterns and anomalies in time series data including unmanned aerial vehicle (UAV) data, stock data, and video data. We will also try to use these patterns to forecast the behavior of the time series in the immediate future. We will further develop techniques to make some optimal or semi-optimal decisions based on the knowledge learned from the data. This research project will introduce or enhance big data analytics of our students who will be faced with big data issues in their future workplace.
- Using linear algebra and geometric techniques to build new algorithms to provide mathematical fundamentals for the development of Machine Learning and AI.
Summer 2022 research project:
- Combating Coronavirus Using Machine Learning: The proposed work will 1) accelerate information extraction from various COVID-19 related datasets by applying Machine Learning (ML) starting with Topic Modeling; 2) improve techniques and accuracy in pursuing knowledge around prevention, treatment and a vaccine via data fusion and model integrations by employing big data analytics and mathematical modeling; and 3) expedite the dissemination of the information and help people around the world to combat coronavirus spread by creating a human-machine interactive webpage, a recommender system, and cell phone apps. The goal is to extract information, integrate models, and create interactive webpages, a recommended system and cell phone apps by employing ML and big data analytics during the 10-week period.
Apply: Email with your unofficial transcript and resume at gu@hmc.edu.
Jamie Haddock
Mathematical Data Science, Numerical Linear Algebra, Optimization, Applied Convex Geometry
Interests center around applications of probability, combinatorics, and convex geometry in data science and optimization. Active areas recently include randomized numerical linear algebra, combinatorial methods for convex optimization, tensor decomposition for topic modeling, and network consensus problems.
Summer 2022 research projects:
- Iterative Methods for Large-scale Systems of Linear Equations: Large-scale systems of linear equations arise in many areas of data science, including in machine learning and as subroutines of several optimization methods. When the systems are very large and cannot be read into working memory in their entirety, iterative methods which use a small portion of the data in each iteration are typically employed. These methods can offer a small memory footprint and good convergence guarantees. Kaczmarz methods, a classical example of these types of methods, consist of sequential orthogonal projections towards the solution set of a single equation (or subsystem). There are many variants within this family of methods, often using randomized or greedy strategies to select the row (subsystem) used in each iteration.There has been a lot of work on Kaczmarz-type methods; some proving convergence results for different variants, some illustrating the application of the Kaczmarz method to specific problems from signal processing, network science, and machine learning, and some developing strategies for systems with adversarial corruption. In this project, we will explore both theoretically and experimentally potential research questions coming from these different areas of Kaczmarz-related study. Potential directions include:
- Developing and analyzing methods for systems with corruption or noise;
- Analyzing methods in the case that the system has structure coming from a graph or network; or
- Developing methods for applications in network ranking and consensus.
- Numerical Linear Algebraic Analyses of Opinion Dynamics on Networks (in collaboration with Prof. Heather Zinn-Brooks): Online social media networks have become extremely influential sources of news and information. Given the large audience and the ease of sharing content online, the content that spreads on online social networks can have important consequences on public opinion, policy, and voting. To better understand the online content spread, mathematical modeling of opinion dynamics is becoming an increasingly popular field of study.
This project focuses on a special class of mathematical models of opinion dynamics on networks called bounded-confidence models. One fundamental question for these models is whether the collection of opinions on the network will converge to a consensus (or other stationary profile) and how quickly that convergence will occur. Many of the mathematical analyses of the dynamics of these models utilize well-known and classical tools from linear algebra and algebraic graph theory. Recently, however, a framework for analysis has been developed that relates the dynamics of these models to iterative methods in numerical linear algebra (Kaczmarz method, Jacobi method, Gauss-Seidel method) and allows for finer-grained analyses of the dynamics via modern numerical algebraic techniques.
In this project, students will relate bounded-confidence models (and variants) to the classical Jacobi and Gauss-Seidel iterative methods (and variants), and will identify directions for novel theoretical convergence analysis of the dynamics of these models. Our group will explore these models both empirically and theoretically, utilizing numerical simulations to guide, develop, and investigate hypotheses for later formal mathematical investigation. - Tensor Models and Methods for Medical Imaging:Large-scale data, such as that from common medical imaging applications, is often naturally multi-modal and represented well by a tensor (a higher-order generalization of a matrix). The mathematics of tensors is notoriously more complex than that of matrices, which has created key gaps in development of tensor-based data analytic techniques, especially in topic modeling and dimensionality reduction. This project will address three main aims:
- To develop tensor-based topic models which respect the natural multi-modal structure of the data and allow for incorporation of flexible expert supervision information;
- To design efficient training methods for tensor-based topic models and produce publicly available open-source implementations; and
- To illustrate the promise of these models and methods in an important case study application to echocardiogram analysis.
In this project, students will generalize common supervised matrix factorization models to tensor data, develop efficient optimization methods for training these models, and produce open-source Python (and/or Matlab) packages for these models/methods. The project will be guided by an application to the cardiac video imaging modality, echocardiograms. In collaboration with cardiologists at UCLA-Harbor Medical Center Department of Cardiology, students will evaluate their models on the novel segmentation application of identifying coherent parts of the echocardiogram. Our team will not only develop novel modeling tools that can utilize information from data experts (e.g., cardiologists), but will work to make these tools and their results available and interpretable to non-model experts.
Apply at: https://uro.hmc.edu
Jon Jacobsen
Student initiated topics are welcome and often some of the most enjoyable thesis projects! A few other project suggestions are outlined below.
- The tacit dimension in learning mathematics: Michael Polanyi’s theory of personal knowledge views all knowledge — regardless of how formalized a discipline’s techniques — as personal in nature, involving processes that rely on an individual’s effort to dwell in particulars and develop an embodied subject coherence from which to attend to knowledge of things seen in its light. Neither the processes nor particulars involved can be entirely specified and this “tacit dimension” lies at the core of all knowledge. In this project we will study learning mathematics through the lens of Polanyi’s theory. Of particular interest are relations to identity, access, achievement, rigor, and one’s sense of belonging with Polanyi’s theory.
- Generalized Julia Sets: Applying Newton’s method to find the roots of a complex polynomial leads to iterating a rational function in the complex plane and the associated theory of Julia sets (fractal boundaries for the basins of attraction). This experimental in nature project would study dynamics for Newton’s method associated with finding roots of vector fields from R^n to R^n, which can be viewed as a generalization of the special R^2 to R^2 case of complex maps. Both situations can be realized as discretizations of a continuous Newton method differential equation. Since we’ve left the realm of complex dynamics, many questions remain including what are the natural candidates for Julia-like sets, their geometric properties (e.g., fractal dimension), relationships between the discrete and continuous problem, and so on. This project would involve significant computational explorations in addition to learning about the theory of complex dynamics.
- Computational models in spatial ecology: this project will require substantial computational skills (esp. matlab) to study population dynamics for integrodifference models in ecology. We have developed a model that allows one to study persistence of a population in terms of calculating the spectral radius of an associated linear operator, however this can be difficult in general and we have established certain alternate metrics that may be equally useful. The researcher would study these models, learn the associated mathematical framework, and develop numerical approaches to better understand their behavior and predictions for persistence in terms of temporal and spatial variations in the model. Of particular importance/challenge is efficient calculation of the metrics and making tools that allow an interested modeler to engage with the models.
Dagan Karp
Algebraic Geometry and Mathematics Education. Dagan Karp’s research is focused on(a)disciplinary research in mathematics, specifically combinatorial algebraic geometry and geometry inspired by theoretical physics, and(b)research in mathematics education. Possible thesis research areas include
- Toric geometry in Gromov-Witten theory, a combinatorial approach to an area of mathematics born from interaction with theoretical physics,
- Tropical geometry, a beautiful combinatorial approach to algebraic geometry, and
- Equity centered pedagogy, rehumanizing, decolonizing, and queering the learning, teaching, and sharing of mathematics.
Prof. Karp also welcomes students with interests in related subjects, and has supervised theses in such subjects as commutative algebra, geometric representation theory, and personalized assessment practices in mathematics education.
Haydee Lindo
More information coming soon.
Susan Martonosi
Summer 2022 research projects:
- Network Analysis of Fake News Propagation on Social Media: We are embedding our previously developed probability model for the propagation of fake news on social media into a network propagation framework. We seek to understand the conditions causing untruthful or highly biased news to “cascade” through the network, and the influence such content has on population beliefs. The work will involve finalizing the existing code base to run simulations through the network, analyzing data, simulating the effect of policy interventions, and drawing conclusions.
- International Pricing of Pediatric Vaccines: GAVI is a Global Vaccine Alliance that facilitates the procurement of pediatric vaccines on behalf of low income countries worldwide. To do so, GAVI negotiates price and quantity contracts directly with vaccine manufacturers. Currently, pentavalent combination vaccines are available that provide, in a single administration, vaccination against five antigens. Under development is a hexavalent vaccine that would add a sixth antigen to the combination vaccine. Doing so would dramatically reduce operational costs associated with distributing these vaccines and could dramatically improve vaccination rates in low income countries. This project seeks to refine our previously developed model to determine procurement prices and quantities to incentivize pharmaceutical companies to develop the hexavalent vaccine. The work will involve developing a code base for the model, running computational analysis over a range of scenarios, analyzing data, simulating the effect of policy interventions, and drawing conclusions.
Apply at: https://uro.hmc.edu
Thesis project possibilities:
Operations research, data analytics, applied probability, homeland security, network optimization, humanitarian logistics.
- Game theory models for pediatric vaccine pricing: Aid organizations like the World Health Organization and the Gates Foundation negotiate prices for pediatric vaccines distributed to low income countries. However, while they try to negotiate as low a price as possible, they also want to ensure sufficient profitability for the vaccine manufacturers so that they will remain in the market, preventing a monopoly for any given vaccine. This problem then becomes a game between the organizations and the vaccine manufacturers. We will use different methods of game theory to find equilibria that can inform policy.
- Fake News: The prevalence and propagation of “fake news” has garnered international attention following the 2016 U.S. presidential election. The mechanisms by which fake and/or biased news articles are propagated are an active area of research, particularly as social media outlets such as Facebook are increasingly being asked to play an active role in fake news detection and deterrence. This proposed research project will develop a probability model and optimization framework to determine the optimal distribution of bias and truthfulness of articles produced by a malicious agent to maximize propagation within a population having known belief distribution. This work will provide insights into the optimal characteristics of biased and/or “fake” news, which can then be used within a game theoretic framework to develop defensive strategies.
- Network disruption methods: Research in this area can involve graph theory, algorithm design, network optimization, operations research, etc.
- Operations research and data analytics techniques applied to a problem of interest to you.
Michael Orrison
Harmonic analysis on finite groups, algebraic voting theory, and applications of the representation theory of finite groups.
Francis Su
Geometric and topological combinatorics, especially as applied to problems in mathematical economics, fair division, voting. This includes: the geometry of triangulations of convex polytopes, intersection problems for convex sets, Sperner’s lemma and and problems from combinatorial topology.
Talithia Williams
Statistical disease modeling, Environmental statistics, Space – time data analysis.
Description
Prevalence and incidence are two important measures of the impact of a disease. For many diseases, incidence is the most useful measure for response planning. We have developed a model to estimate incidence of progressive diseases, with an application to cataract disease in Africa. Initial results suggest different behavior of unilateral and bilateral incidence that might teach us something about the normal course of cataract disease. For example, how long before people with unilateral cataract usually develop bilateral cataract? Does this time depend on age, geographic region, gender or other factors that influence unilateral incidence? There are several natural extensions to this current body of work that would make for an exciting thesis project.
Possible Thesis Projects
- Developing a data clustering methodology.
- Modeling age-dependent mortality due to cataract.
- Applying the current model to other progressive diseases, such as cancer.
- Developing a model that incorporates factors that influence cataracts (i.e. diabetes in the population)
Darryl Yong
Mathematics education, applied mathematics, perturbation theory, partial differential equations
Heather Zinn-Brooks
Summer 2022 research projects:
- Mathematical models of opinion dynamics on networks: Online social media networks have become extremely influential sources of news and information. Given the large audience and the ease of sharing content online, the content that spreads on online social networks can have important consequences on public opinion, policy, and voting. To better understand the online content spread, mathematical modeling of opinion dynamics is becoming an increasingly popular field of study.These summer projects focus on a special class of mathematical models of opinion dynamics on networks called bounded-confidence models. An area of interest in my research group is characterizing the dynamics of bounded-confidence models whose outcomes are driven primarily by key agents in the system (which have distinct properties as compared to the remaining agents). This is particularly well-suited to study by mechanistic models, where we can explicitly control inputs, apply techniques from dynamical systems and network theory, and carefully highlight underlying assumptions.Possible project directions:
- Tuning media impact: Via Monte Carlo simulations of an agent-based bounded-confidence network model, we could investigate strategies for depolarization of synthetic networks and quantify conditions under which polarization and depolarization occur in these networks. We can also explore the effects of more realistic media forcing drawn from Twitter data on the activity of media outlets.
- Competition, cooperation, and influence maximization of information cascades: Messages in an online social network are not spreading in a vacuum; they are competing and interacting with other active messages on the network. Under what conditions do we expect the messages to “compete”? When will one message be limited by another? When will they spread independently? Modeling the context under which messages are affected by multiple cooperating or competing diffusion processes is an important extension of online content spreading models. Another interesting potential direction is to explore is how the choice of seed node affects the properties of the resulting dissemination tree (e.g., number of messages spread, width, and diameter).
- Parameter fitting and sensitivity analysis for information cascades: While members of my group generally study these questions from a theoretical perspective, we are also motivated by modeling the spread of information in real-world networks. In this project, the student would use Twitter retweet data to fit parameters our information cascade models. Given these data, we would extraction information about the resulting dissemination tree and use parameter fitting techniques and perform a sensitivity analysis as a means to validate or invalidate existing models.
- Other projects in mathematical modeling of complex systems: I am open to and excited about other projects in math modeling and dynamical systems with biological and social applications. Active research directions include mathematical modeling of gender representation in mathematics, polarization in two-party political systems, pattern formation and agent-based models in biological systems, and more (see website). If you are interested in a project in along one of these lines, feel free to “pitch” your project idea.
- Numerical Linear Algebraic Analyses of Opinion Dynamics on Networks (in collaboration with Prof. Jamie Haddock): Online social media networks have become extremely influential sources of news and information. Given the large audience and the ease of sharing content online, the content that spreads on online social networks can have important consequences on public opinion, policy, and voting. To better understand the online content spread, mathematical modeling of opinion dynamics is becoming an increasingly popular field of study.
This project focuses on a special class of mathematical models of opinion dynamics on networks called bounded-confidence models. One fundamental question for these models is whether the collection of opinions on the network will converge to a consensus (or other stationary profile) and how quickly that convergence will occur. Many of the mathematical analyses of the dynamics of these models utilize well-known and classical tools from linear algebra and algebraic graph theory. Recently, however, a framework for analysis has been developed that relates the dynamics of these models to iterative methods in numerical linear algebra (Kaczmarz method, Jacobi method, Gauss-Seidel method) and allows for finer-grained analyses of the dynamics via modern numerical algebraic techniques.
In this project, students will relate bounded-confidence models (and variants) to the classical Jacobi and Gauss-Seidel iterative methods (and variants), and will identify directions for novel theoretical convergence analysis of the dynamics of these models. Our group will explore these models both empirically and theoretically, utilizing numerical simulations to guide, develop, and investigate hypotheses for later formal mathematical investigation.
Apply at: Undergraduate Research Opportunities